1001. Grid Illumination-网格照明

在大小为n x n的网格grid上，每个单元格都有一盏灯，最初灯都处于关闭状态。

给你一个由灯的位置组成的二维数组lamps，其中lamps[i] = [rowi, coli]表示打开位于grid[rowi][coli]的灯。即便同一盏灯可能在lamps中多次列出，不会影响这盏灯处于打开状态。

当一盏灯处于打开状态，它将会照亮自身所在单元格以及同一行、同一列和两条对角线上的所有其他单元格。

另给你一个二维数组queries，其中queries[j] = [rowj, colj]。对于第j个查询，如果单元格[rowj, colj]是被照亮的，则查询结果为1，否则为0。在第j次查询之后按照查询的顺序 ，关闭位于单元格grid[rowj][colj]上及相邻 8 个方向上（与单元格grid[rowi][coli]共享角或边）的任何灯。

返回一个整数数组ans作为答案，ans[j]应等于第j次查询queries[j]的结果，1表示照亮，0表示未照亮。

示例 1：

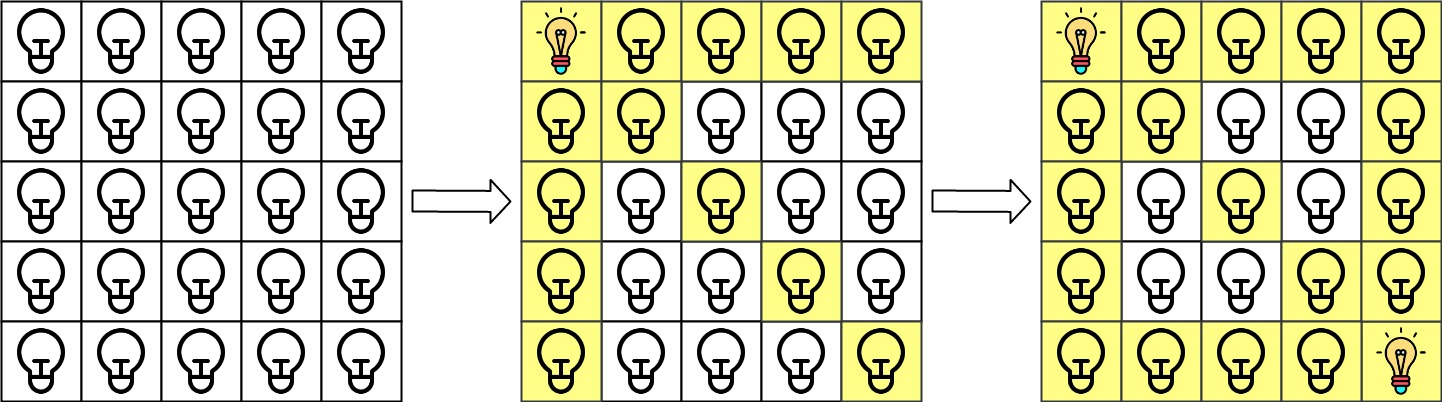
输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
输出：[1,0]
解释：最初所有灯都是关闭的。在执行查询之前，打开位于 [0, 0] 和 [4, 4] 的灯。第 0 次查询检查 grid[1][1] 是否被照亮（蓝色方框）。该单元格被照亮，所以 ans[0] = 1 。然后，关闭红色方框中的所有灯。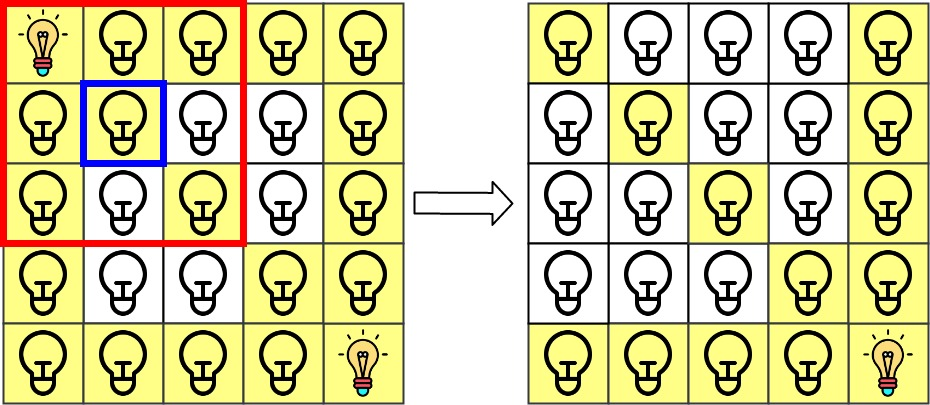

第 1 次查询检查 grid[1][0] 是否被照亮（蓝色方框）。该单元格没有被照亮，所以 ans[1] = 0 。然后，关闭红色矩形中的所有灯。

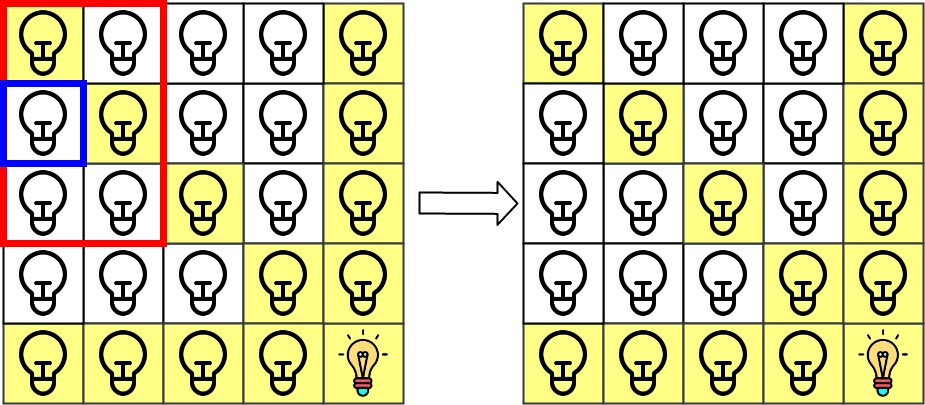
示例 2：

输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
输出：[1,1]

示例 3：

输入：n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
输出：[1,1,0]

提示：

• 1 <= n <= 10^9
• 0 <= lamps.length <= 20000
• 0 <= queries.length <= 20000
• lamps[i].length == 2
• 0 <= row_i, col_i < n
• queries[j].length == 2
• 0 <= row_j, col_j < n

Python:

import collections
class Solution:
    def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:
        row, col = defaultdict(int), defaultdict(int)
        dia, rdia = defaultdict(int), defaultdict(int)
        aset = set()
        for (x, y) in lamps:
            if (x, y) not in aset:
                aset.add((x, y))
                row[x] += 1
                col[y] += 1
                dia[x-y+n-1] += 1
                rdia[x+y] += 1
        result = [0 for i in range(len(queries))]
        for i, (x,y) in enumerate(queries):
            if row[x] > 0 or col[y] > 0 or dia[x-y+n-1] > 0 or rdia[x+y] > 0:
                result[i] = 1

            for a in range(x-1, x+2):
                for b in range(y-1, y+2):
                    if 0 <= a < n and 0 <= b < n and (a, b) in aset:
                        aset.remove((a,b))
                        row[a] -= 1
                        col[b] -= 1
                        dia[a-b+n-1] -= 1
                        rdia[a+b] -= 1
        return result

Java:

class Solution {
    public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {
        Set<List<Integer>> aset = new HashSet<>();
        Map<Integer, Integer> row = new HashMap<>();
        Map<Integer, Integer> col = new HashMap<>();
        Map<Integer, Integer> dia = new HashMap<>();
        Map<Integer, Integer> rdia = new HashMap<>();

        for(int[] a: lamps)
        {
            List<Integer> arr = Arrays.asList(a[0], a[1]);
            if(!aset.contains(arr))
            {
                aset.add(arr);
                int x = a[0];
                int y = a[1];
                row.put(x, row.getOrDefault(x, 0)+1);
                col.put(y, col.getOrDefault(y, 0)+1);
                dia.put(x-y, dia.getOrDefault(x-y, 0)+1);
                rdia.put(x+y, rdia.getOrDefault(x+y, 0)+1);
            }
        }
        int[] result = new int[queries.length];
        for(int k = 0; k < queries.length; k++)
        {
            int x = queries[k][0];
            int y = queries[k][1];
            if(row.getOrDefault(x, 0) > 0 || col.getOrDefault(y, 0) > 0 || dia.getOrDefault(x-y, 0) > 0 || rdia.getOrDefault(x+y, 0) > 0)
            {
                result[k] = 1;
            }
            for(int i = x-1; i < x+2; i++)
            {
                for(int j = y-1; j < y+2; j++)
                {
                    List<Integer> temp = Arrays.asList(i, j);
                    if(i >= 0 && i < n && j >= 0 && j < n && aset.contains(temp))
                    {
                        aset.remove(temp);
                        row.compute(i, (key,v)->v-=1);
                        col.compute(j, (key,v)->v-=1);
                        dia.compute(i-j, (key,v)->v-=1);
                        rdia.compute(i+j, (key,v)->v-=1);
                    }
                }
            }
        }
        return result;
    }
}